On The Matter Of Space

Preface

The new version of my paper is now formulated as an $sl(4,\mathbb{R})$ gaugetheory.

Content Overview

This website, along with my blog, is primarily a vehicle for promulgating my “An Already-Unified Gauge Theory“, AAGT. This page is a quick overview with little in-depth explanations and even less mathematics. That can all be found in the above link.

The Theory – Some Mathematical Consequences

First and foremost – space is massive. That’s right – it has mass (parenthetically 🙂 for the experts, by way of a scalar density which is called Lorentz invariant). How do we know? Simply because we observe the extra gravity and can find nothing there – except space. It has quite a low density, about the order of magnitude of the average cosmic density, + or -, varying with location. If we add up all its mass in our solar system, we calculate too little to measure in comparison with the sun and planets. But if we take a huge volume, like our galaxy, its gravity is quite detectable: we call this Dark Matter (DM) where there is an over-density, Dark Energy (DE) where there is an under-density.
All forces can be represented simply as (tensor) fields of event displacements, 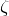$\zeta$ , shifts of events in spacetime. This is a gauge transformation; the Lie group 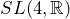$SL(4,\mathbb{R})$ contains the algebra of the SM. It also contains gravity. It is the group of 4-volume preserving gauges of the metric.
These fields of displacement are gauge transformations of the metric tensor, $\overline{g}=e^{\zeta}\,g\,e^{\zeta}$ .
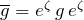Quantum field theory (QFT) is a linear (Hilbert space) representation of these same fields.
Different forces are represented by gauge tensors with different analytic and algebraic properties.
Gravity is a symmetric gauge tensor – locally it can be diagonalized and normalized meaning gravity disappears in free-fall, as is known.
Electromagnetism is an anti-symmetric gauge – cannot be made to disappear by a local (real) change of reference, as is known.
Gauge field components must satisfy Special Relativity (Klein-Gordon equation e.g.) since they are flat space fields.
Empty space is not empty, 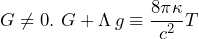$G\neq 0.\,\,G +\Lambda\,g\equiv \dfrac{8\pi\kappa}{c^2}T$ , a scalar field, the Dark Matter field, a massive spacetime.
The Einstein field equation becomes an identity, 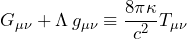$G_{\mu\nu}+\Lambda\,g_{\mu\nu}\equiv \dfrac{8\pi\kappa}{c^2}T_{\mu\nu}$ , where T, instead of containing all non-gravitational energy, now contains only gravitational energy – in covariant form.
Matter and spacetime are made of the same “stuff” – gravitational energy; particles are where spacetime is dense, i.e. gravitational energy large.
Special Relativity, through the Klein-Gordon equation with a mass’s local gravitational field coupled to its inertial (i.e. quantum) field, gives the gauge field for that mass.
The Lagrangian action is stationary when a gravitational mass pulls just enough inertia from the Dark Matter field to avoid singularity. (The CERN data show this – a linear relation between particle mass and the Higgs coupling constant.) This both gives rise to inertia and eliminates singularity.
Mach’s principle – inertia given by the integral of the gauge field over all space.
Singularities are removed from the theory automatically – no more pathological infinities.
Black holes lose their singularities.
The gravitational radiation solution is identical to the TT-mode Isaacson tensor, only exact and covariant.
EM radiation fields give 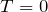$T=0$ . They propagate along geodesics, but they are not a source of gravity. This is not true for general EM fields.
Magnetic monopoles cannot exist – vortices are closed in realistic topologies.
Dark Matter is pure, bosonic, undifferentiated matter and arises automatically.
Galaxy rotation curves are matched from theory without the need for density profile models.
Baryon-lepton symmetry is speculated.
– Check out my paper.

The Famous Singularity

Let’s face it. Despite the famous singularity theorems, singularities in General Relativity (GR) are a problem. Einstein thought so and so do many physicists in that field today. The theorems are not wrong, just irrelevant, their basic assumptions not being applicable. The observables of spacetime are distance and duration. They are specified by the metric tensor. Anywhere the metric tensor is infinite those observables are undefined. That is, the theory does not work there and cannot provide information about such regions. Up till now no one has been able to find a way around this problem. Indeed there are many proofs about the singularities. One hears statements about them being an inherent property of the theory, or even worse, of the universe itself. All this certainty about singularities, and all the while there is not even a theory of matter for GR. After all, it is the matter that causes the curvature. The theory of matter comes from Quantum Theory (QT) and it is not “compatible” with GR. So how does matter get into GR? Check out my paper.

Thermodynamic Equation of State

Enough discrete points can be modelled by a continuous object.

Just as elsewhere in physics, a continuum thermodynamic approach is used to handle the large aggregates of elementary particles and fields found in celestial bodies. In terms of the singularity, this introduces two problems. First, these models may rely on equations of state that come from outside GR. Any relationship of density and pressure based on EM or QT must be assumed to be valid in a covariant form – and belong on the right hand side of the Einstein equation. Also, since there is not at present a unified field theory, it is not clear that such a relationship is valid in intense gravitational fields at all. Basically it comes down to what to put on the right side of the Einstein equation. If there is a unified field, then only putting all sources of non-gravitational energy on the right side is just wrong regardless of equation of state, that being a fundamentally non-covariant choice for a unified theory. What is the covariant choice? Check out my paper.

If Only …

If only a multiplicative small potential rather than an additive one was used when first obtaining an approximate solution to the General Relativistic field equation, then the landscape of GR might be completely different. Consider the gravitational field of a spherically symmetric mass in the weak field, low velocity limit. The metric tensor only has one significant component, the $g _{0 0}$ element. It is $1+\dfrac{2\Phi(r)}{c^2}$ where $\Phi(r)$ is the classical gravitational potential. Anyone first studying GR finds the factor of 2 curious. Also $\Phi<0$ since gravity is an attractive force. This means that the whole metric term can vanish at large enough potential. This was also seen as a curiosity historically. However, since $e^{2 \Phi (r)}\approx1+2 \Phi (r)$ for small $\Phi(r)$ , it solves to the same approximation also; $G=0$ to second order in the mass for $\Phi(r)=-m/r$ . Now the factor of 2 becomes clear. Second rank metric transformations are multiplied twice with the transformation matrix – once on each side so to speak. So what we have is

$ds^2=g_{\mu \nu}dx^{\mu}dx^{\nu}}\longrightarrow \bar{g}_{\mu \nu }dx^{\mu }dx^{\nu }=\left(e^{\Phi }\right)_{\lambda }^{\mu }g_{\mu \nu }\left(e^{\Phi }\right)_{\tau }^{\nu }\right)dx^{\lambda }dx^{\tau }=g_{\lambda \tau }d\bar{x}^{\lambda }d\bar{x}^{\tau }.$

This can either be viewed as a gauge transformation of the metric or equally well as a transformation of coordinates, leaving the metric unchanged. That is, it is not a usual coordinate transformation. So the math alone tells us how gravity enters the theory even though we were just looking at an approximation. The second thing the math tells us is that the density is not exactly zero, $G\neq0$ , so an empty space around a mass is just an approximation. If you want to see how $\Phi(r)$ or any other “field” naturally finds its place in the gauge tensor, check out my paper.

Boundary Condition

So why would you use a multiplicative factor rather than an additive term to the metric? The answer is the boundary condition. The solution to any differential equation like the Einstein equation, $G_{\mu\nu}\equiv \dfrac{8\pi\kappa}{c^2}T_{\mu\nu}$ , depends upon the boundary condition. The boundary condition for the potential, $\Phi(r)$ , in both cases is the same; it goes to $0$ for large $r$ . However this gives rise to different boundary conditions on $G$ , and therefore $T$ . The additive case gives $T=0$ while he multiplicative case gives $T\neq0$ . Also, we know $T=0$ is wrong. Whether you consider Dark Matter or the quantum vacuum, empty space is not empty. This also means using the Schwarzchild solution for non-empty “empty space” is wrong . It is only an approximation to set $T=0$ . This is the source of the pathological singularity, the black hole and non-covariant gravitational energy. In fact the gravitational energy that permeates all space is the same as dark matter and the quantum vacuum. All are fluctuating “zero-point” fields. Check out my paper.

Inertia

So if $T\neq0$ outside a massive body, in empty space, that means empty space has mass, though just not as dense as in a ponderable massive body like a proton, planet or star. So should not you be able to detect this matter? You do. Every time you try to move a massive object it resists the effort. That resistance is called inertia. Once in motion an object stays in motion. That is due to relativity. Space has whatever properties are necessary to provide a resistance to acceleration, but it is agnostic when it comes to speed – all speeds are equivalent. This is because all objects must obey the Klein-Gordon equation, a necessity of relativity.

This Little Change

This one little change – a multiplicative field rather than an additive one – both unifies the fields and removes singularities. It removes singularity because no value for the potential can drive the metric to zero or infinity. It unifies the fields since the obvious generalization is to use any/all classical or quantum fields as metric gauge fields. Actually this entire line of reasoning was prompted by using the EM field as a gauge field in the first place. See how it happened. Check out my paper.

I f we simply use $e^{2 \Phi (r)}$ rather than $1+2 \Phi (r)$ to do the approximation – all is revealed.

Spacetime Twists and Flows

The Maxwell equations of electromagnetism are also equations of something that twists and flows. This was promptly noted by many physicists who tried to do then what I am doing now. They, however, did not benefit from what we now know is a geometrically dynamic spacetime. They still tried building such models and looking for a “luminiferous aether” permeating space to serve as a medium for such dynamics. All the detail is found in my paper, “On the Matter of Space:An Already-Unified sl(4, R) Invariant Gauge Theory”. Check it out.

Spacetime Squeezes and Stretches

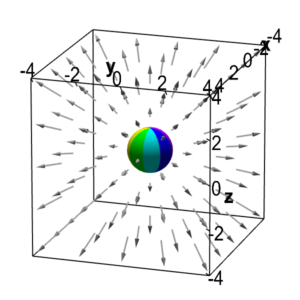
Gravity is thought of as the bending and stretching of spacetime. This is specified by the metric tensor. There is a dual complementarianism here. First the metric tensor is a symmetric tensor. Symmetric tensors are used in deformable media and in geometry to depict compression (or rarefaction) and shear. This is in contrast to anti-symmetric tensors which describe rotations. One of Einstein’s attempts to unify gravity and electromagnetism was to consider non-symmetric metric tensors because of these facts. Still today physicists are looking for extra degrees of freedom to fit all the forces together. Want to see how they fit together just using physics “as is”? Check out my paper.

Pages: 1 2